1. 회귀문제 기울기
- 손실함수에 대한 가중치와 편향의 미분값이다.
1. 회귀문제 설정
- 손실함수: 오차제곱합
- 은닉층 활성화 함수: 시그모이드
- 출력층 활성화 함수: 항등 함수
2. 출력층의 기울기
- 손실함수를 출력층의 출력값으로 미분한 값이다.
- 역전파 알고리즘에 사용되며 이를 이용해 역방향으로 기울기를 전파해 가중치와 편향을 업데이트한다.
3. 은닉층 기울기
- 출력층과 마찬가지로 손실함수를 은닉층의 출력값으로 미분한 것이다.
- 은닉층 기울기도 역전파 알고리즘에 사용되며 모델의 가중치를 업데이트해 회귀모델에 최적화되도록 학습한다.
2. 분류문제 기울기
1. 회귀문제 설정
- 손실함수: 교차 엔트로피
- 은닉층 활성화 함수: 시그모이드
- 출력층 활성화 함수: 소프트 맥스
2. 출력층의 기울기
- 손실함수를 출력값으로 미분한다. 역전파 알고리즘에 적용해, 모델의 가중치를 업데이트해 분류 모델이 최적화 되도록 학습한다.
3. 은닉층 기울기
- 기울기를 구할때 체인룰을 사용한다. 모든층의 가중치를 업데이트하고, 분류모델이 최적화 되도록 학습한다.
3. 최적화 알고리즘
1. 최적화 알고리즘(옵티마이저)
- 경사 하강법은 기본적으로 기울기를 바탕으로 가중치와 편향을 조금씩 조정한다.
- 위 과정을 반복해 정답과의 오차가 최소화 되도록 신경망을 최적화한다.

2. 확률적 경사 하강법(SGD)
- 가중치와 편향을 수정하기 위해 반복학습시 전체 샘플 데이터를 사용하지 않는다.
- 무작위로 추출한 일부 샘플 데이터를 사용한다.
- 가중치와 편항을 수정하는 방법은 학습률을 사용하는 기존 경사 하강법과 동일하다.
[1] 장점
1) 전체 샘플 대신 일부 샘플을 사용해 전체 하습 시간이 단축된다.
2) 무작위로 샘플을 선택하기 때문에 국소 최저점에 잘 빠지지 않는다.
[2] 단점
1) 학습의 진행과정에 따른 파라미터의 수정량을 유연하게 조정할수 없음
2) 국소 최저점에 빠지는 경우가 발생한다.
3. 모멘텀

[1] 장점
기존 SGD 대비 지역(국소) 최저점에 잘 빠지지 않는다.
[2] 단점
학습률외에 모멘텀 상수까지, 조정해야할 파라미터가 생긴다.
4. 아다그라드
- 학습이 진행되면서 알고리즘에 의해 학습률이 감소함

- 첫번째 식에서 최초 h는 0, 학습이 진행되면서 증가
- 두번째 식에서 h가 분모에 있으므로, 전체 값은 학습이 진행되면서 수정량이 감소한다.
- 처음에는 넓은 영역에서 탐색을 시작, 점차 탐색범위를 좁혀가며 효율적인 동작을 한다.
[1] 장점
조정해야할 파라미터가 n(학습률)밖에 없다.
[2] 단점
1) 파라미터별로 수정량이 계속 감소해 최적화 도중 수정량이 0이 될수도 있다.
2) 수정량이 0이 되면 파라미터는 더 이상 학습이 진행되지 않는다.
5. RMSProp
- 아다그라드는 학습이 진행되며 학습률이 0에 수렴하는 현상이 발생해서 이를 극복하기 위해 만들어졌다.
- 기울기를 같은 비율로 누적하지 않고 지수이동평균을 활용한다.
- 가장 최근의 기울기를 많이 반영하고 먼 과거의 기울기는 조금 반영한다.
6. Adam
- 모멘텀과 아다그라드를 융합한 방법이다.
4. 배치
1. 에포크(epoch)
- 모든 훈련 데이터를 1회 학습하는 것을 1에포크하고 한다.
- 훈련 데이터의 샘플을 여러개 묶어 학습에 사용한다.
- 훈련 샘플 그룹을 배치하고 한다.
- 1에포크는 다수의 배치로 구성된다.
2. 배치

- 배치 사이즈는 하나의 배치에 포함되는 샘플의 수이다.
- 하나의 배치에 포함된 모든 샘플을 사용해 가중치와 편향을 수정한다.
- 배치 사이즈는 학습 중에 일정하다.
3. 배치 학습
- 배치 사이즈는 전체 훈련 데이터의 수이다.
- 1에포크마다 전체 훈련 데이터의 오차 평균과 개별 가중치별 기울기 합을 구한다.
- 평균오차와 기울기 합을 이용해 가중치와 편향을 수정한다.
- 계산량이 적은 장점이 있지만 지역 최저점이 빠지기 쉽다.

- 훈련 데이터의 수를 N, 개별 데이터의 오차를 Ei라고 할 경우, 오차는 위와 같다.

- 개별 가중치의 기울기는 다음과 같다.
- 훈련 데이터의 샘플 수가 1000개일 경우, 배치 사이즈는 1000, 1에포크에 가중치와 편향은 1회수정한다.
4. 온라인 학습
- 배치 사이즈가 1
- 개별 샘플마다 가중치와 편향을 수정한다.
- Outlier의 영향을 받아 안정성이 떨어진다.
- 지역 최저점이 빠지는 것을 어느정도 막아준다.
- 훈련 데이터의 샘플수가 1000개일 경우 배치사이즈가가 1이고 1에포크에 가중치와 편향을 1000회 수정한다.
5. 미니 배치
- 훈련 데이터를 작은 그룹(배치)으로 분할하고, 이 그룹마다 가중치와 편향을 수정한다.
- 온라인 학습에 비해 배치사이즈가 크기때문에 Outlier에 대한 민감도가 적다.
- 전체 훈련 데이터의 수를 N, 배치사이즈를 n(n<=N)이라 할때, 아래처럼 정의된다.
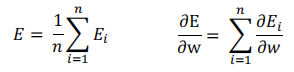
6. 배치 적용
- 배치 사이즈는 정해져 있지 않지만 일반적으로 10~100사이로 적용된다.
5. 행렬 연산 순전파
1. 순전파

- 은닉층에서 출력층으로 순전파이다.
- 은닉층의 뉴런수가 입력 m개, 출력수는 n개, 배치 사이즈는 h이다.
u = np.dot(x, w) + b
y = 1 / (1+np.exp(-u))- 층의 출력을 Y라 할때 h * n이다. 즉, 배치 사이즈 X 출력 뉴런 수 행렬이 된다.
- numpy를 사용해 정리하고 활성화 함수가 시그모이드일때 위에 처럼 적용한다.
6. 행렬 연산 역전파
1. 가중치 기울기 행렬
grad_w = np.dot(x.T, delta)- grad_w는 가중치 기울기 행렬, x는 입력 행렬, delta는 \( \delta \)행렬 \(\Delta \)를 나타낸다.
2. 편향 기울기 행렬
grad_b = np.sum(delta, axis=0)3. 출력 기울기 행렬
grad_x = np.dot(delta, w.T)- 결과 행렬의 각 원소는 현재 층에 있는 모든 뉴런의 결과를 합한 것이다.
7. tensorflow
- 텐서플로우는 다양한 작업에대해 데이터 흐름 프로그래밍을 위한 오픈소스 소프트웨어 라이브러리이다. 심볼릭 수학 라이브러리이자, 인공 신경망같은 기계 학습 응용프로그램 및 딥러닝에도 사용된다.
1. 설치하기

- 자신이 사용하는 작업환경으로 아동한후(p39-env) conda install tensorflow를 입력해 텐서플로우를 설치한다.
2. 예제 1
- 작업 하려는 경로에 해당 csv 파일을 위치시킨다.
[1] 모듈 선언, csv파일 로드
from tensorflow.keras import models, layers
#케라스: 딥러닝 라이브러리, 텐서플로우를 비롯한 다양한 딥러닝 백엔드를 지원한다.
#케라스 라이브러리에서 모델, 레이어를 임포트한다.
import numpy as np
#넘파이 라이브러리를 임포트한다.data_set = np.loadtxt('data/ThoraricSurgery3.csv',delimiter=',')
data_set
#csv파일을 임포트한다.--> 결과
array([[ 1. , 2.88, 2.16, ..., 0. , 60. , 0. ],
[ 2. , 3.4 , 1.88, ..., 0. , 51. , 0. ],
[ 2. , 2.76, 2.08, ..., 0. , 59. , 0. ],
...,
[ 2. , 3.04, 2.08, ..., 0. , 52. , 0. ],
[ 2. , 1.96, 1.68, ..., 0. , 79. , 0. ],
[ 2. , 4.72, 3.56, ..., 0. , 51. , 0. ]])[2] 데이터선언, 신경망 정의
X = data_set[:, :16]#입력 데이터로 사용될 특성(피처)이다.
y = data_set[:, 16]#타겟 데이터로 사용될 레이블(정답)이다.model = models.Sequential()
#인공신경망 정의
model.add(layers.Dense(30, input_dim=16, activation='relu'))
#입력 16개, 출력 30개 그리고 활성화 함수가 relu인 모델 선언
model.add(layers.Dense(1, activation='sigmoid'))
# 입력은 30개 출력이 1개이고 sigmoid 활성화 함수를 사용하는 모델을 선언한다.model.summary()--> 결과
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 30) 510
dense_1 (Dense) (None, 1) 31
=================================================================
Total params: 541
Trainable params: 541
Non-trainable params: 0
_________________________________________________________________[3] 모델 컴파일
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 외우기, 케라스에서 제공하는 이진 분류형
# 손실함수 binary_crossentropy, 옵티마이저 adam, 평가지표 accuracy로 컴파일한다.history = model.fit(X,y,epochs=5, batch_size=16)
#손실과 정확도를 기록한다.
#배치사이즈는 16개, 에포크는 5개이다.--> 결과
Epoch 1/5
30/30 [==============================] - 1s 1ms/step - loss: 0.4436 - accuracy: 0.8426
Epoch 2/5
30/30 [==============================] - 0s 1ms/step - loss: 0.4414 - accuracy: 0.8553
Epoch 3/5
30/30 [==============================] - 0s 1ms/step - loss: 0.4337 - accuracy: 0.8468
Epoch 4/5
30/30 [==============================] - 0s 1ms/step - loss: 0.4299 - accuracy: 0.8489
Epoch 5/5
30/30 [==============================] - 0s 1ms/step - loss: 0.4238 - accuracy: 0.84683. 예제 2
[1] 모듈 선언
from tensorflow.keras import models, layers
import numpy as np
import tensorflow as tf[2] csv로드, 데이터
data_set = np.loadtxt('data/ThoraricSurgery3.csv',delimiter=',')
#csv로드
X = data_set[:, :16]
#입력데이터 입력
y = data_set[:, 16]
#타겟 데이터 입력[3] 모델이름, 배치사이즈, 뉴런 선언
model_name = 'thoraric_surgery'
#모델 이름을 지정한다.
batch_size = 16
#배치사이즈를 지정한다.
param = {
'model_name':model_name,
'input_dim':16,
'hidden_dim':30,
'output_dim':1
}
#입력 16개, 은닉 30개, 출력 1개의 뉴런을 지정한다.[4] 모델 클래스 정의
class ThoraricSurgery(tf.keras.Model):
# 텐서플로우의 tf.keras.Model클래스를 상속받아 새로운 모델의 정의한다.
def __init__(self, **kargs):
super(ThoraricSurgery, self).__init__(name=kargs['model_name'])
self.fc1 = layers.Dense(kargs['hidden_dim'],input_dim=kargs['input_dim'],
activation='relu')
self.fc2 = layers.Dense(kargs['output_dim'], activation='sigmoid')
#__init__메소드는 위의 param이라는 하이퍼파리미터로 받아와 모델 구조를 만든다.
def call(self, x):
x = self.fc1(x)
x = self.fc2(x)
return x
#순전파를 정의한다. x데이터를 받아 fc1과 fc2를 통과시켜 예측값을 출력한다.model = ThoraricSurgery(**param)[5] 모델 컴파일
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 외우기, 케라스에서 제공하는 이진 분류형history = model.fit(X,y,epochs=10, batch_size=16)--> 결과
Epoch 1/10
30/30 [==============================] - 1s 1ms/step - loss: 7.5061 - accuracy: 0.1553
Epoch 2/10
30/30 [==============================] - 0s 1ms/step - loss: 0.7010 - accuracy: 0.7043
Epoch 3/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4949 - accuracy: 0.8511
Epoch 4/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4455 - accuracy: 0.8511
Epoch 5/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4437 - accuracy: 0.8511
Epoch 6/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4449 - accuracy: 0.8511
Epoch 7/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4423 - accuracy: 0.8511
Epoch 8/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4378 - accuracy: 0.8511
Epoch 9/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4331 - accuracy: 0.8511
Epoch 10/10
30/30 [==============================] - 0s 1ms/step - loss: 0.4314 - accuracy: 0.8511
8. PyTorch
- PyTorch는 Python을 위한 오픈소스 머신 러닝 라이브러리이다. Torch를 기반으로 하며, 자연어 처리와 같은 애플리케이션을 위해 사용된다. GPU사용이 가능하기 때문에 속도가 상당히 빠르다.
1. 설치하기
[1] PyTorch 사이트로 이동한다.

PyTorch
An open source machine learning framework that accelerates the path from research prototyping to production deployment.
pytorch.org
[2] 아래쪽으로 스크롤한다음 다음처럼 선택한다. 자신이 작업하는 환경에 맞추어 주면 된다. 그리고 Compute Platform은 GPU성능을 따라가기 때문에 내장 그래픽일 경우 CPU를 권장한다.

[3] 텐서플로우처럼 자신의 작업환경에 입력후 설치를 진행한다.

9. Regression 예제
import numpy as np
import matplotlib.pyplot as plt
#모듈 임포트input_data = np.arange(0,np.pi*2,0.1)
#입력데이터로 0부터 2π까지 0.1 간격으로 값을 가지는 배열이다.
correct_data = np.sin(input_data)
#input_data에 대한 결과값으로 sin함수를 적용했다.
input_data = (input_data - np.pi) / np.pi
# 입력데이터 범위를 -1.0 ~ 1.0로 지정한다.
#신경망 도델 입력 데이터가 -1.0~1.0,0~1.0범위로 정규화 되기 때문이다.
n_data = len(correct_data)
#데이터의 개수를 나타낸다.n_in = 1
#입력 뉴런 개수
n_mid=5
#은닉 뉴런 개수
n_out = 1
#출력뉴런 개수wb_width = 0.01
#가중치(weight), 편향(bias)을 초기화하는데 사용된다.
eta = 0.1
#학습룰을 나타내는 변수이다.
epoch = 2001
#학습데이터를 몇번 반복할지 정하는 변수이다.
interval = 200
#학습중 일정간격으로 손식(loss)을 출력하기 위한 변수이다.class MiddleLayer:
#은닉층을 정의하고 있는 클래스이다.
def __init__(self, n_upper, n): #n_upper: 이전층의 출력크기, n: 현재 층 출력의 크기
self.w = wb_width*np.random.randn(n_upper, n)
#가중치를 나타내는 변수이다.
#현재층의 입력과 이전 층의 출력을 연결한다.
self.b = wb_width*np.random.randn(n)
#편향을 나타내는 변수이다.
#입력에 항상 더해지는 상수이다.
def forward(self, x):
self.x = x
u = np.dot(x, self.w)+self.b
self.y = 1 / (1 + np.exp(-u))
#순전차를 수행한다.
#입력과 가중치의 내적을 구하고 편향을 더한다.
#그 다음 시그모이드 함수를 적용해 y를 계산한다.
def backward(self, grad_y):
delta = grad_y * (1-self.y)*self.y
self.grad_w = np.dot(self.x.T, delta)
self.grad_b = np.sum(delta)
self.grad_x = np.dot(delta, self.w.T)
#역전파를 수행한다.
#grad_y: 순전파의 출력에 대한 손실함수의 기울기이다.
#grad_w: 가중치에 대한 기울기이다. 입력데이터의 전치(T, 행과 열을 바꾼 연산)와 delta와 내적을 계산해 구한다.
#grad_b: 편향에 대한 기울기이다. delta의 합을 계산해 구한다.
#grad_x: 입력데이터에 대한 기울기이다. delta와 가중치의 전치(T)를 내적해 구한다.
def update(self,eta):
self.w -= eta * self.grad_w
self.b -= eta * self.grad_b
#가중치와 편향을 업데이트 한다.
#역전파로 계산된 기울기와 학습률을 이용해 가중치와 편향을 수정한다.class OutputLayer:
#출력층을 나타내는 클래스이다.
def __init__(self, n_upper, n): #n_upper: 이전층의 출력크기, n: 현재 층 출력의 크기
#클래스 초기화 함수
self.w = wb_width*np.random.randn(n_upper, n)
self.b = wb_width*np.random.randn(n)
#n_upper와 n을 받아서 가중치와 편향을 랜덤한 값으로 초기화한다.
def forward(self, x):
#입력 데이터 x를 받아 순전파를 수행한다.
self.x = x
u = np.dot(x, self.w)+self.b
#입력데이터 x와 가중치의 내적에 편향값을 더한다.
self.y = u
#최종 예측값
def backward(self, t):
#목표값 t를 받아 역전파를 수행한다.
delta = self.y-t
#출력값과 타겟값의 오차를 계산한다.
self.grad_w = np.dot(self.x.T, delta)
#가중치의 기울기를 계산한다.
self.grad_b = np.sum(delta)
#편행의 기울기를 계산한다.
self.grad_x = np.dot(delta, self.w.T)
#입력데이터의 기울기를 계산한다.
def update(self,eta):
self.w -= eta * self.grad_w #가중치 업데이트
self.b -= eta * self.grad_b #편향 업데이트middle_layer = MiddleLayer(n_in, n_mid)
#입력뉴런, 은닉 뉴런을 입력한다.
output_layer = OutputLayer(n_mid, n_out)
#은닉뉴런, 출력 뉴런을 입력한다.for i in range(epoch):
#학습과정을 몇번 반복할지 작성한다.
index_random = np.arange(n_data)
np.random.shuffle(index_random)
#핸덤으로 데이터인덱스를 섞어 데이터 사용순서를 무작위화한다.
total_error = 0
plot_x=[]
plot_y=[]
for idx in index_random:
#섞인 데이터 순서대로 데이터를 가지고와 순전파와 역전파를 진행한다.
x=input_data[idx]
t=correct_data[idx]
middle_layer.forward(x.reshape(1,1))
output_layer.forward(middle_layer.y)
#입력데이터를 은닉층으로 전달하고 출력을 다시 출력층으로 전달해 예측을 생성한다.
output_layer.backward(t.reshape(1,1))
middle_layer.backward(output_layer.grad_x)
#출력층의 예측과 실제값간의 차이를 계산해 역전파를 수행한다.
middle_layer.update(eta)
output_layer.update(eta)
#은닉층의 역전파를 진행해 은닉층의 가중치와 편향을 갱신한다.
if i%interval == 0:
#학습진행하는 동안 일정 간격으로 그래프를 그리고 오차를 계산한다.
y=output_layer.y.reshape(-1)
#출력층의 출력값을 1차원 배열로 변환한다.
total_error += 1.0/2.0 * np.sum(np.square(y-t))
#출력값 y와 정답값 t간의 오차를 계산해 더해준다.
plot_x.append(x)
plot_y.append(y)
if i % interval == 0:
# 출력 그래프 표시
plt.plot(input_data, correct_data, linestyle="dashed")
plt.scatter(plot_x, plot_y, marker="+")
plt.show()
# 에포크 수와 오차 표시
print("Epoch:" + str(i) + "/" + str(epoch), "Error:" + str(total_error/n_data))--> 결과





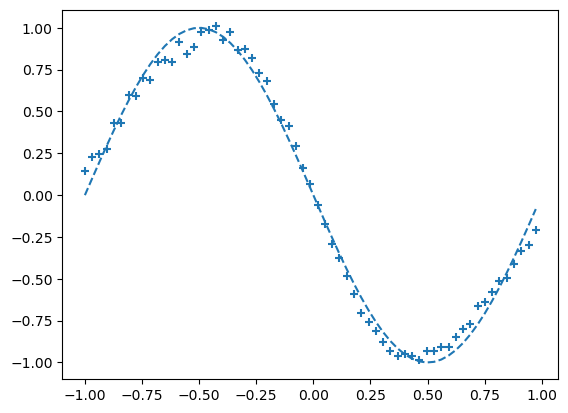
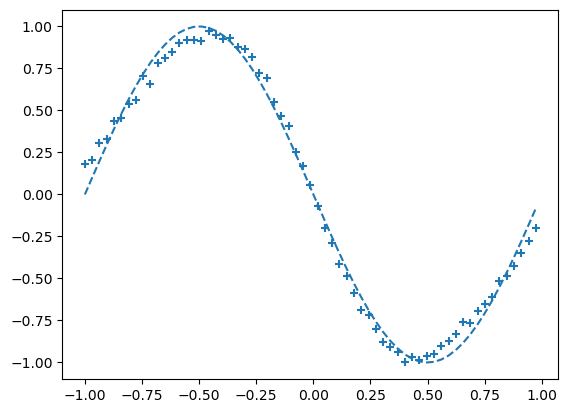


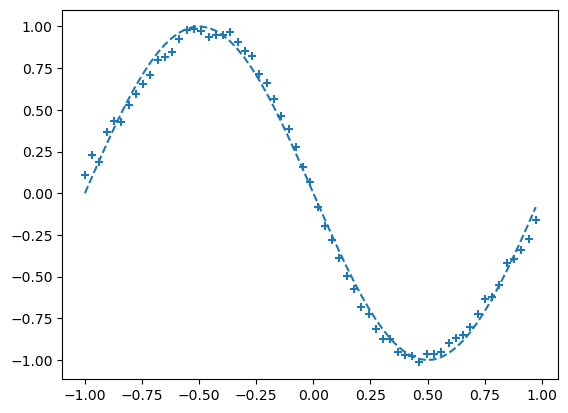

- 점점 +가 그래프 모양과 닮아간다. 이는 신경망 모델이 점차적으로 데이터 패턴을 학습헤 예측을 개선하가는 과정을 나타낸 것이다.
10. classification 예제
import numpy as np
import matplotlib.pyplot as plt
#모듈 임포트X = np.arange(-1.0, 1.1, 0.1)
Y = np.arange(-1.0, 1.1, 0.1)
#-1.0에서 1.1까지 범위를 설정하고 0.1 간격으로 값을 생성한다.input_data = []
correct_data = []
for x in X:
for y in Y:
input_data.append([x,y])
#input_data에 X,Y의 조합인 [x,y]가 입력된다.
if y< np.sin(np.pi * x):
correct_data.append([0,1])
#y의 값이 np.sin(np.pi*x)보다 작으면[0,1]을 넣는다.
else:
correct_data.append([1,0])
#y의 값이 np.sin(np.pi*x)보다 크거나 같으면 [1.0]을 넣는다.- 이렇게 입력데이터(input_data)와 정답데이터(correct_data)를 만들어 신경망에 사용한다.
n_data = len(input_data)
#input_data의 개수를 저장한다.
input_data = np.array(input_data)
correct_data = np.array(correct_data)
#입력과 정답데이터를 Numpy 배열로 변환한다.n_in=2
#입력층의 뉴런개수
n_mid=6
#은닉층의 뉴런개수
n_out=2
#출력층의 뉴런개수wb_width = 0.01
#가중치와 편향 초기화 시 사용되는 범위
eta = 0.1
#학습률, 가중치 갱신시 적용되는 학습속도
epoch = 101
#학습 반복횟수
interval = 10
#에포크를 몇번 반복할때마다 그래프 그릴지 설정class MiddleLayer:
def __init__(self, n_upper, n): #n_upper: 이전층의 출력크기, n: 현재 층 출력의 크기
self.w = wb_width*np.random.randn(n_upper, n)
self.b = wb_width*np.random.randn(n)
def forward(self, x):
self.x = x
u = np.dot(x, self.w)+self.b
self.y = 1 / (1 + np.exp(-u))
def backward(self, grad_y):
delta = grad_y * (1-self.y)*self.y
self.grad_w = np.dot(self.x.T, delta)
self.grad_b = np.sum(delta)
self.grad_x = np.dot(delta, self.w.T)
def update(self,eta):
self.w -= eta * self.grad_w
self.b -= eta * self.grad_bclass OutputLayer:
def __init__(self, n_upper, n): #n_upper: 이전층의 출력크기, n: 현재 층 출력의 크기
self.w = wb_width*np.random.randn(n_upper, n)
self.b = wb_width*np.random.randn(n)
def forward(self, x):
self.x = x
u = np.dot(x, self.w)+self.b
self.y = np.exp(u)/np.sum(np.exp(u),axis=1,keepdims=True)
#np.exp(u)의 각 행에 대해 원소들의 합을 계산하고 keepdims=True로 이를 유지한 상태로 출력한다.
#이를 통해 확률 분포를 만든다.
def backward(self, t):
delta = self.y-t
self.grad_w = np.dot(self.x.T, delta)
self.grad_b = np.sum(delta)
self.grad_x = np.dot(delta, self.w.T)
def update(self,eta):
self.w -= eta * self.grad_w
self.b -= eta * self.grad_bmiddle_layer = MiddleLayer(n_in, n_mid)
output_layer = OutputLayer(n_mid, n_out)sin_data = np.sin(np.pi * X)
for i in range(epoch):
index_random = np.arange(n_data)
np.random.shuffle(index_random)
total_error = 0
x_1=[]
y_1=[]
x_2=[]
y_2=[]
#출력 그래프를 그리기 위한 데이터를 모으는 리스트이다.
for idx in index_random:
x=input_data[idx]
t=correct_data[idx]
middle_layer.forward(x.reshape(1,2))
output_layer.forward(middle_layer.y)
output_layer.backward(t.reshape(1,2))
middle_layer.backward(output_layer.grad_x)
middle_layer.update(eta)
output_layer.update(eta)
if i%interval == 0:
y=output_layer.y.reshape(-1)
total_error += - np.sum(t*np.log(y+1e-7))
if y[0] > y[1]:
x_1.append(x[0])
y_1.append(x[1])
else:
x_2.append(x[0])
y_2.append(x[1])
if i % interval == 0:
# 출력 그래프 표시
plt.plot(X, sin_data, linestyle="dashed")
plt.scatter(x_1, y_1, marker="+")
plt.scatter(x_2, y_2, marker="x")
plt.show()
# 에포크 수와 오차 표시
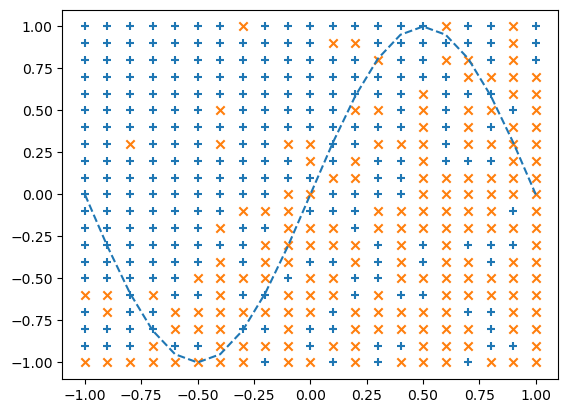
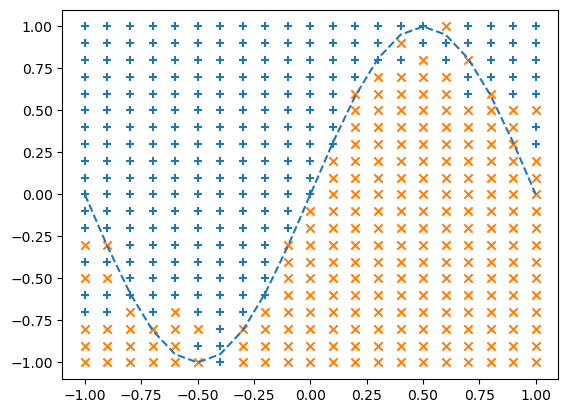
print("Epoch:" + str(i) + "/" + str(epoch), "Error:" + str(total_error/n_data))- 출력 그래프는 에포크가 알정 간격으로 그려진다. 각 클래스에 속하는 데이토 포트인트는 'x_1', 'y_1'리스트와 'x_2','y_2'리스트에 추가되어 분류경계를 표시하게된다.
--> 결과









'비트교육센터 > AI' 카테고리의 다른 글
| [비트교육센터][AI] 7일차 이미지분석 (0) | 2023.08.10 |
|---|---|
| [비트교육센터][AI] 6일차 데이터 예측하기 (0) | 2023.08.09 |
| [비트교육센터][AI] AI 5일차 과적합, K겹 교차 검증 (0) | 2023.08.05 |
| [비트교육센터][AI] AI 4일차 Pytorch, 다중분류 (0) | 2023.08.04 |
| [비트교육센터][AI] AI 2일차 기초수학, 뉴런, 순전파, 역전파, 은닉층, 출력층 (0) | 2023.08.02 |