[비트교육센터][AI] AI 1일차 머신러닝, 딥러닝

비트교육센터/AI

[비트교육센터][AI] AI 1일차 머신러닝, 딥러닝

달의요정루나 2023. 8. 1. 01:11

1. 머신러닝

- 컴퓨터가 데이터를 학습하고 경험을 통해 스스로 문제를 해결하는 기술이다.

1. Iris 품종분류

## Iris 품종분류  
a. Iris의 품종의 측정 데이터 존재
- setosa, versicolor, virginica
- (꽃잎)pertal length, petal width
- (꽃받침) sepal length, sepal width

b. 품종별 측정데이터를 이용해 새로 채집한 iris의 품종을 예측하는 ML 모델을 제작  
c. 품종별 측정데이터가 이미 존재하므로 지도학습(supervised learning)  
d. 3개의 품종 중 하나를 예측하는 문제이므로 분류(classification) 문제  
e. 입력 특성값을 feature(4개), 결과값을 class(3개의 class) 라 함  
f. 한 개의 꽃에 대한 측정값(sample)을 한 개의 품종으로 출력, 이 때 출력값(품종)을 Label 이라 함

[1] Iris 데이터셋 불러오기

from sklearn.datasets import load_iris

# Iris 데이터셋 불러오기
iris_dataset = load_iris()

# 데이터 셋의 속성 확인하기
print(iris_dataset.keys())

--> 결과

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

- data: 입력데이터를 담고 있는 배열, 각 샘플의 특성들로 이루어진 2차원 배열이다.

- target: 레이블을 담고 있는 배열로 각 샘플에 대한 분류값(0,1,2)으로 이루어진 1차원 배열이다.

- target_names: 레이블의 이름을 담고 있는 배열로 분류값(0,1,2)에 해당하는 클래스 이름이다.

- DESCR: 데이터셋에 대한 간략한 설명을 담고 있는 문자열이다.

- feature_names: 특성의 이름을 담고 있는 배열로 입력데이터의 각 열에 해당하는 특성의 이름이다.

- filename: 데이터셋 파일의 경로를 나타내는 문자열이다.

[2] Iris 데이터, DESCR

print(iris_dataset['DESCR'])

- 데이터셋에 대한 간략한 설명을 담은 문자열이다.

--> 결과

.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

[3] Iris 데이터, target_names

print(iris_dataset['target_names'])

- Iris 데이터셋의 레이블(target)에 해당하는 클래스의 이름들을 담고 있는 배열을 반환한다.

--> 결과

['setosa' 'versicolor' 'virginica']

[4] Iris 데이터, feature_names

print(iris_dataset['feature_names'])

- Iris 데이터 셋의 특성에 해당하는 이름들을 담고 있는 리스트를 반환한다.

--> 결과

['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

[5] Iris 데이터, 딕셔너리 키 가져오기

print(iris_dataset.keys())

- Iris 데이터셋의 정보를 담고 있는 딕셔너리의 키들을 반환한다.

--> 결과

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

[6] Iris 데이터, type()

print(type(iris_dataset['data']))

- data의 타입을 출력하면 NumPy배열 임을 알 수 있다.

--> 결과

<class 'numpy.ndarray'>

[7] Iris 데이터, shape

print(iris_dataset['data'].shape)

- iris 데이터의 차원과 크기를 말해준다. 2차원 배열이며 데이터 포인트가 150개, 각 데이터 포인트는 4개의 특성으로 구성되어 있다.

--> 결과

(150, 4)

[8] Iris 데이터, head부터 5개 출력하기

print(iris_dataset['data'][:5])

- 처음 5개 데이터 포인트를 출력할 수 있다.

- 결과에서 각 행은 하나의 데이터 포인트를 나타내며, 4개의 열은 해당 데이터 포인트의 특성 값들을 나타낸다.

- 각 데이터 포인트는 순서대로 "꽃받침 길이", "꽃받침 폭", "꽃잎 길이", "꽃잎 폭"을 나타내는 4개의 특성 값을 가지고 있다.

--> 결과

[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]

[9] Iris 데이터, target변수 형태

print(iris_dataset['target'].shape)

- 1차원 배열이고 길이가 150인 배열을 의미한다.(150개의 데이터 포인트로 이루어져 있다.)

--> 결과

(150,)

[10] Iris 데이터, target변수

print(iris_dataset['target'])

- 꽃의 품종을 나타내는 타겟 변수(레이블)를 담고 있는 NumPy 배열이다.

- 0은 Setosa 품종, 1은 Versicolor 품종, 2는 Virginica 품종을 의미한다.

--> 결과

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

2. 성과 측정

a. 머신러닝 모델을 구축해 새로운 데이터의 품종을 예측해야 함
b. 훈련데이터는 평가에 사용할 수 없음(모델이 훈련하는 동안 데이터를 기억함)
c. 150개의 sample을 training set 과 test set으로 나누어야 함

scikit-learn의 train_test_split 함수를 사용하여 데이터를 나눔
데이터는 대문자 X, 레이블을 소문자 y로 표기
train_test_split 함수의 test_size 값을 0.0 ~ 1.0 사이로 지정할 수 있음, 지정하지 않으면 train set = 0.75, test set = 0.25로 기본 지정됨
random_state 값은 랜덤 seed(0 ~ 42)

[1] mglearn라이브러리 설치

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = \
    train_test_split(iris_dataset['data'],iris_dataset['target'],random_state=0)

- train_test_split 함수는 데이터를 학습 데이터와 테스트 데이터로 나누어주는 함수로, 머신러닝 모델을 학습하고 성능을 평가하는데 사용된다.

- test_size 매개변수를 지정하지 않았으므로 기본값인 0.25로 설정된다.(전체 데이터의 25퍼를 사용한다는 의미이다.)

- random_state=0: 데이터를 무작위로 섞을 때 사용되는 시드 값을 고정한다. 이렇게 해서 실행시 동일한 학습 및 테스트 데이터셋이 생성된다.

- 함수의 반환값을 총 4개이다.

x_train: 학습 데이터의 특성(Feature) 배열
x_test: 테스트 데이터의 특성(Feature) 배열
y_train: 학습 데이터의 타겟(Target) 변수 배열
y_test: 테스트 데이터의 타겟(Target) 변수 배열

[2] 반환값

print(x_train.shape)

--> 결과

(112, 4)

print(y_train.shape)

--> 결과

(112,)

print(x_test.shape)
print(y_test.shape)

--> 결과

(38, 4)
(38,)

[3] scatter matrix

- mglearn 라이브러리의 산점 행렬을 생성한다. 여러 특성들 간의 산점도를 시각화해 서로의 관계를 파악할 수 있도록 도와준다.

머신러닝 모델을 구축하기 전에 데이터를 조사해야 함(머신러닝이 필요한 지, 누락된 정보가 있는지...)
scatter matrix 를 이용해 데이터 확인
pip install mglearn, 저자(Andreas C Müller)가 만든 라이브러리
결과를 보면 세 개의 클래스가 petal과 sepal의 length/width 에 따라 잘 구분되어짐을 확인

import pandas as pd
import mglearn
import matplotlib.pyplot as plt

iris_dataframe = pd.DataFrame(x_train, columns=iris_dataset.feature_names)
pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15,15), marker='o', 
                           hist_kwds={'bins':20}, s=60, alpha=.8, cmap=mglearn.cm3)
plt.show()

- iris_dataframe: x_train 데이터를 pandas DataFrame으로 변환한 뒤 산점 행렬로 그린다.

- pd.plotting.scatter_matrix: 해당함수를 이용해 iris_dataframe의 산점 행렬을 생성한다.

1) c파라미터: y_train으로 설정해 꽃의 품종에 따라 데이터 포인트의 색상을 구분

2) figsize: 플롯의 크기를 조정

3) marker: 데이터 포인트의 마커 스타일을 설정

4) hist_kwds: 대각선에 표시된 히스토그램의 bin 개수를 설정

5) s: 데이터 포인트의 크기를 조정

6) alpha: 데이터 포인트의 투명도 조절

7) cmap: 데이터 포인트의 색상을 지정하는 데 사용되는 컬러맵 설정

--> 결과

3. K-최근접 이웃 알고리즘

훈련 데이터를 저장하여 생성
새로운 데이터에 대한 예측은 가장 가까운 훈련 데이터의 포인트를 찾아서 결정
훈련데이터에서 새로운 데이터 포인트에 가장 가까운 k개의 이웃을 찾음
위에서 찾은 이웃들의 클래스 중 빈도가 가장 높은 클래스를 예측값으로 사용(자세한 내용은 2장에서), 이 예제에서는 하나의 이웃만 사용

[1] 최근접 이웃 생성하기

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)

- KNeighborsClassifier: scikit-learn 라이브러리에서 제공하는 k최근접 이웃 분류기이다.

- n_neighbors=1: 이웃의 수를 1로 설정한 knn 분류기를 생성한다.

knn.fit(x_train,y_train)

- knn은 새로운 데이터 포인트가 주어졌을때, 해당 데이터 포인트와 가장 가까운 훈련 데이터 포인트들 중에서 다수결 투표를 통해 분류하는 간단한 분류 알고리즘이다.

- x_train데이터와 y_train데이터로 학습을 시켜 새로운 데이터를 예측할 수 있다.

--> 결과

[2] 예측하기

예측하기
sepal length/wifth = 5/2.9, petal length/width = 1/0.2
위 데이터를 Numpy 2차원 배열로 생성

1) 데이터포인트 구성

import numpy as np
x_new = np.array([[5, 2.9, 1, 0.2]])
print(x_new.shape)

- numpy로 구성된 새로운 데이터 포인트이다. 1개의 샘플에 4개의 특성(꽃받침 길이, 꽃받침 폭, 꽃잎 길이, 꽃잎 폭)으로 구성되어 있다.

--> 결과

(1, 4)

2) 예측결과 저장

prediction = knn.predict(x_new)
print(prediction)

- x_new에 해당하는 붓꽃의 종류를 예측한 결과를 prediction에 저장한다.

--> 결과

[0]

- 0이 나오면 첫번째 붓꽃이름을 출력할 수 있다.

3) 붓꽃이름 출력

print(iris_dataset['target_names'][0])

- 첫번째 붓꽃이름을 출력한다.

--> 결과

['setosa']

4) 샘플 출력

print(x_train[:5]) #x_train 배열의 처음 5개 출력
print(y_train[:5]) #y_train 배열의 처음 5개 출력

--> 결과

[[5.9 3.  4.2 1.5]
 [5.8 2.6 4.  1.2]
 [6.8 3.  5.5 2.1]
 [4.7 3.2 1.3 0.2]
 [6.9 3.1 5.1 2.3]]

[1 1 2 0 2]

5) 예측결과

y_pred=knn.predict(x_test)
print(y_pred)

- x_test에 대해 knn 분류기를 사용한 예측결과이다.

--> 결과

[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2]

6) 정확도 계산1

print("Test Accuracy: {:.2f}".format( np.mean(y_pred == y_test) ))

- np.mean에서 예측된 타겟 테이블 y_pred와 실제 타겟 레이블 y_test를 비교해 맞춘 비율을 계산한다.

--> 결과

Test Accuracy: 0.97

7) 정확도 계산2

x_train, x_test, y_train, y_test = train_test_split(iris_dataset['data'], iris_dataset['target'], random_state=0)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(x_train, y_train)
print("test set에 대한 정확도: {:.2f}".format(knn.score(x_test, y_test)))

- train_test_split: iris데이터셋을 훈련세트와 테스트 세트로 나눈다.

- KneighborsClassifier를 초기화하고 이웃의 수를 1로 설정한다.

- knn.fit을 사용해 훈련세트에 대해 분류기를 학습시킨다.

- knn.score를 사용해 테스트 세트에 대한 정확도를 평가한다.

--> 결과

test set에 대한 정확도: 0.97

2. 딥러닝

- 인공신경망을 기반으로 하는 머신러닝의 한 분야이다. 인간 뇌의 뉴런 동작방식을 통해 구성된 모델로 복잡한 문제를 해결할 수 있다.

1. 분류와 회귀

분류
a. 분류는 미리 정의된 가능성 있는 여러 클래스 레이블 중 하나를 예측
b. 두 개의 클래스로 분류하는 건 이진 분류(binary classification), 셋 이상의 클래스로 분류하는 건 다중 분류(multiclass classification) 이라 함
회귀
a. 연속적인 숫자(실수)를 예측
b. 사람의 교육 수준, 나이, 주거지를 바탕으로 연간 소득을 예측 또는 특정 농산물의 올 해 수확량 예측
c. 분류문제와 달리 회귀문제에서는 출력값의 작은 차이는 문제가 되지 않음

2. 일반화, 과대적합, 과소적합

지도학습에서 훈련 데이터로 학습한 모델이 훈련 데이터와 특성이 같다면 처음 보는 새로운 데이터가 주어져도 정확히 예측할 수 있음
모델이 처음 보는 데이터에 대해 정확하게 예측할 수 있다면 이를 훈련 세트에서 테스트 세트로 일반화(generalization)되었다고 함
보유하고 있는 모든 정보를 이용해 만든 복잡한 모델은 훈련 세트에만 최적화되어 새로운 데이터에 일반화 되기 어렵다. 이를 과대적합(overfitting)이라 함
(45세 이상이고, 자녀가 셋 미만이며 이혼하지 않은 고객은 요트를 살 것이다.)
모델이 너무 간단하면 데이터의 다양성을 잡아내지 못하고 정확도도 떨어짐, 이를 과소적합(underfitting)이라 함 (집이 있는 사람은 모두 요트를 사려고 함)
모델이란, 수학적 알고리즘의 표현식

다음 그림과 같이 일반화 성능이 최대가 되는 최적점에 있는 모델을 찾아야 함

데이터 세트에 다양한 데이터 포인트가 많을수록(feature의 수가 많을수록) 과대적합 없이 더 복잡한 모델을 구축할 수 있음

3. 지도 학습 알고리즘

예제에 사용할 데이터 셋
a. forge 데이터셋은 인위적으로 만든 이진 분류 데이터셋 feature 2개, target 1

x축은 첫 번째 특성, y축은 두 번째 특성으로 그래프 작성

[1] 이진 분류 데이터셋 생성

import mglearn
import matplotlib.pyplot as plt

X, y = mglearn.datasets.make_forge()
print(X)
print(y)

- mglearn.datasets.make_forge(): 이 함수는 인공적으로 만든 이진 분류 데이터셋을 생성한다. 2개의 특성을 가진 26개의 데이터 포인트로 이루어져 있다. 각 데이터 포인트는 2개의 클래스(0 또는 1) 중 하나에 속하며, x는 특성 데이터, y는 해당 데이터 포인트의 클래스 레이블을 나타낸다.

--> 결과

[[ 9.96346605  4.59676542]
 [11.0329545  -0.16816717]
 [11.54155807  5.21116083]
 [ 8.69289001  1.54322016]
 [ 8.1062269   4.28695977]
 [ 8.30988863  4.80623966]
 [11.93027136  4.64866327]
 [ 9.67284681 -0.20283165]
 [ 8.34810316  5.13415623]
 [ 8.67494727  4.47573059]
 [ 9.17748385  5.09283177]
 [10.24028948  2.45544401]
 [ 8.68937095  1.48709629]
 [ 8.92229526 -0.63993225]
 [ 9.49123469  4.33224792]
 [ 9.25694192  5.13284858]
 [ 7.99815287  4.8525051 ]
 [ 8.18378052  1.29564214]
 [ 8.7337095   2.49162431]
 [ 9.32298256  5.09840649]
 [10.06393839  0.99078055]
 [ 9.50048972 -0.26430318]
 [ 8.34468785  1.63824349]
 [ 9.50169345  1.93824624]
 [ 9.15072323  5.49832246]
 [11.563957    1.3389402 ]]
[1 0 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0 0 1 0 0 0 0 1 0]

[2] 산점도 만들기

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["Class 0", "Class 1"], loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
print("X.shape:", X.shape)

- mglearn.discrete_scatter() 함수는 데이터셋을 산점도(scatter plot)로 시각화하는 함수이다.

- X[:,0]은 데이터셋의 첫번째 특성값, X[:,1]은 데이터셋의 두번째 특성값, y는 데이터 포인트의 클래스 레이블(0,1)을 나타낸다.

--> 결과

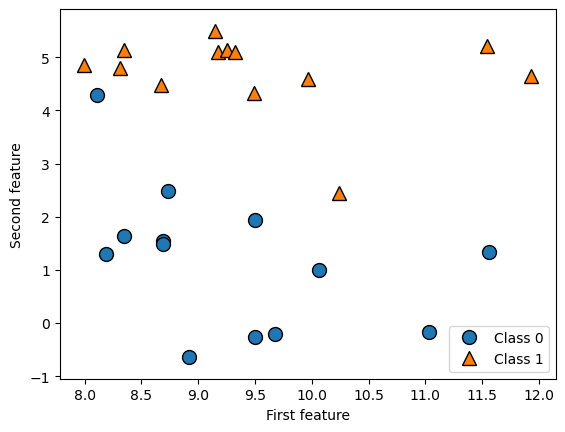
X.shape: (26, 2)

[3] wave 데이터 셋

b. 회귀 알고리즘에는 인위적으로 만든 wave 데이터셋을 사용

입력 특성 한 개와 target 변수를 가짐
특성을 x축, target을 y축

X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.ylim(-3, 3)
plt.xlabel("Feature")
plt.ylabel("Target")
plt.show()

- mglearn.datasets.make_wave함수: 임의의 1차원 데이터셋을 만드는 함수이다. 1개의 특성과 연속적인 타겟값을 가진다.

- x축은 특성, y축은 target을 가지며 plt.ylim(-3,3)은 y축의 범위를 -3~3으로 설정한다.

--> 결과

[4] 위스콘신 유방암 데이터셋

c. scikit-learn 에 들어 있는 실제 데이터셋 사용

유방암 종양의 임상 데이터를 기록해 놓은 위스콘신 유방암 데이터 셋(cancer)
각 종양은 양성(benign)과 악성(malignant)로 레이블 되어 있음
조직 데이터를 기반으로 종양이 악성인지를 예측하도록 학습하는 것이 과제

1) 유방암 데이터셋 로드하기

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys():\n", cancer.keys())

- scikit-learn에서 기본으로 제공하는 데이터셋이다.

--> 결과

cancer.keys():
 dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])

2) 데이터 형태 출력

print("유방암 데이터의 형태:", cancer.data.shape)

- cancer.data: 유방암 데이터셋의 특성 데이터를 담고 있는 배열이다. shape를 붙이면 형태를 보여준다.

--> 결과

유방암 데이터의 형태: (569, 30)

3) 샘플 수 출력

import numpy as np

print("클래스별 샘플 수:\n{}".format({n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))
#np.bincount : 배열 내 각 occurrence 수

- cancer.target: 유방암 데이터셋의 레이블 정보를 가지고 있다.

- np.bincount(cancer.target): cancer.target 배열 내에서 각 클래스의 개수를 센다.

- 그러면 악성 샘플수, 양성샘플수가 출력된다.

- zip은 악성과 양성 클래스 이름과 샘플수를 쌍으로 묶어준다.

--> 결과

클래스별 샘플 수:
{'malignant': 212, 'benign': 357}

4) 특징 배열 출력하기

print("Feature names:\n{}".format(cancer.feature_names))

- 유방암 데이터셋의 특징들의 이름을 나타내는 배열이다. 30개의 특징이 있으면 유방암 세포의 특징을 나타내는데 사용된다.

--> 결과

Feature names:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']

4. K-NN

a. k-Nearest Neighbors

k-NN은 가장 가까운 훈련 데이터 샘플을 최근접 이웃으로 찾아 예측에 사용

[1] 최근접 시각화

1) 이웃 개수 1개

mglearn.plots.plot_knn_classification(n_neighbors=1)

--> 결과

2) 이웃개수 3개

mglearn.plots.plot_knn_classification(n_neighbors=3)

--> 결과

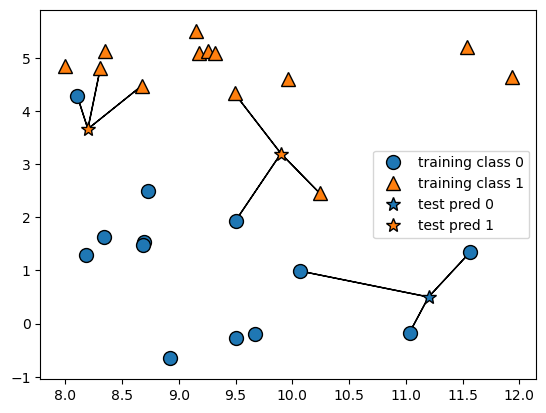
[2] make_forge()

from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

- make_forge(): 인위적으로 생성된 이진 분류용 데이터 셋을 만들어준다.

- 데이터 셋을 만들고 train_test_split함수로 데이터를 훈련세트와 데스트 세트로 분할한다.

- x는 데이터의 특성을 담은 Numpy배열, y는 데이터의 클래스 레이블을 담은 Numpy배열, random_state는 난수 시드값으로, 매번 동일한 데이터를 생성한다.

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)

- 이웃개수가 3개인 knn분류기를 선언한다.

clf.fit(X_train, y_train)

- fit메소드로 knn을 훈련데이터로 학습시킨다.

--> 결과

print("Test set accuracy: {:.2f}".format(clf.score(X_test, y_test)))

- 테스터 데이터의 정확도를 계산한다.

--> 결과

Test set accuracy: 0.86

5. KNeighborsClassifier 분석

2차원 데이터셋이므로 가능한 모든 테스트 포인트의 예측을 xy평면에 그려봄
각 데이터 포인트가 속한 클래스에 따라 평면에 색을 칠하여 결정 경계(decision boundary)를 확인함
다음은 이웃이 하나, 셋, 아홉 개일 때의 결정 경계를 보여줌

[1] 분류기 생성

fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
    # the fit method returns the object self, so we can instantiate
    # and fit in one line
    clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
    
axes[0].legend(loc=3)
plt.show()

- knn을 사용해 1개, 3개, 9개의 이웃을 가진 분류기를 생성한다.

--> 결과

이웃을 하나 선택했을 때는 결정 경계가 훈련 데이터에 가깝게 따라감
이웃의 수를 늘릴 수록 결정 경계는 더 부드러워짐, 부드러운 경계는 더 단순한 모델을 의미
이웃을 적게 사용하면 모델의 복잡도가 증가(Overfitting), 많이 사용하면 복잡도는 감소(Underfitting)
훈련 데이터 전체 수를 이웃의 수로 지정하는 극단적인 경우, 모든 테스트 포인트가 같은 이웃을 가지므로 테스트 포인트에 대한 예측은 모두 같은 값이 나옴
즉 훈련 세트에서 가장 많은 데이터 포인트를 가진 클래스가 예측값이 됨

[2] 세트의 성능 평가하기

모델의 복잡도와 일반화 사이의 관계를 입증해 봄
실제 데이터인 유방암 데이터셋을 사용
훈련 세트와 테스트 세트로 나눔
이웃의 수를 달리하면서 훈련 세트와 테스트 세트의 성능을 평가함

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=66)
# stratify : 이 옵션을 target으로 지정하면 train, test set으로 분리할 때 각 클래스(양성, 음성) 비율을 유지하게 함

training_accuracy = []
test_accuracy = []

# try n_neighbors from 1 to 10
neighbors_settings = range(1, 11)

for n_neighbors in neighbors_settings:
    # build the model
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train, y_train)
    
    # record training set accuracy
    training_accuracy.append(clf.score(X_train, y_train))
    
    # record generalization accuracy
    test_accuracy.append(clf.score(X_test, y_test))
    
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()
plt.show()

- 유방암 데이터셋을 생성하고, knn을 사용해 학습한다.

- 1~10까지의 이웃개수에 대해 학습 및 평가를 수행해, 각각 이웃의 개수에 따른 학습 정확도와 일반화 정확도를 기록해 그래프로 시각화한다.

--> 결과

Overfitting과 Underfitting의 특징을 잘 보여줌
최근접 이웃의 수가 하나일 때는 훈련 데이터에 대한 예측이 완벽
이웃의 수가 늘어나면 모델은 단순해지고 훈련 데이터의 정확도는 감소
이웃을 하나 사용한 테스트 세트의 정확도는 이웃을 많이 사용했을 때보다 낮음
1-NN 이 모델을 너무 복잡하게 만든다는 것을 설명함
10-NN 은 모델이 너무 단순해서 정확도는 떨어짐
정확도가 가장 좋을 때는 중간 정도인 6-NN 임

[3] 회귀분석

wave 데이터 셋을 이용해서 회귀분석에 사용
x 축에 세 개의 테스트 데이터를 흐린 별 모양으로 표시
최근접 이웃을 한 개만 이용할 때 예측은 그냥 가장 가까운 이웃의 target 값임

1) 이웃갯수 1개

mglearn.plots.plot_knn_regression(n_neighbors=1)

- k-최근접 이웃회귀 모델을 시각화한다. 입력데이터와 가장 가까준 k개의 이웃들의 평균 또는 가중평균을 사용해 예측값을 계산한다. k가 1인 경우의 knn회귀 모델을 시각화한다.

--> 결과

2) 이웃갯수 3개

mglearn.plots.plot_knn_regression(n_neighbors=3)

--> 결과

[4] knn 회귀 모델 구현

from sklearn.neighbors import KNeighborsRegressor

X, y = mglearn.datasets.make_wave(n_samples=40)

# split the wave dataset into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# instantiate the model and set the number of neighbors to consider to 3
reg = KNeighborsRegressor(n_neighbors=3)

# fit the model using the training data and training targets
reg.fit(X_train, y_train)

- mglearn.datasets.make_wave 함수로 생성한 데이터를 사용하여 k-최근접 이웃 회귀 모델을 학습하고 평가하는 과정을 보여준다.

- mglearn.datasets.make_wave(n_samples=40)을 사용해 wave 데이터를 생성한다. x는 입력데이터, y는 타겟데이터이다.

- train_test_split: 데이터를 학습용과 테스트용으로 분할한다.

- KneighborsRegressor(n_neighbors=3): knn회귀모델 객체 'reg'를 생성해 가장 가까운 이웃 3개를 사용해 예측한다.

- reg.fit: 모델을 학습한다. x_train, y_train을 사용해 모델의 파라미터를 조정하고 입력 데이터와 타겟데이터 간의 관계를 학습한다.

--> 결과

from sklearn.neighbors import KNeighborsRegressor
reg = KNeighborsRegressor(n_neighbors=3)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))

# create 1,000 data points, evenly spaced between -3 and 3
line = np.linspace(-3, 3, 1000).reshape(-1, 1)

for n_neighbors, ax in zip([1, 3, 9], axes):
    # make predictions using 1, 3, or 9 neighbors
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train, y_train)
    ax.plot(line, reg.predict(line))
    ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
    ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
    ax.set_title(
        "{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
        n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")
    
axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best")
plt.show()

- knn회귀 모델을 이웃의 수로 학습한 결과를 시각화 했다.

- KNeighborsRegressor(n_neighbors=3): k-최근접 이웃 회귀 모델 객체 reg를 생성한다. 이 모델은 가장 가까운 이웃 3개를 사용하여 예측한다.

- np.linspace(-3, 3, 1000).reshape(-1, 1): -3부터 3까지 1000개의 데이터 포인트를 생성하고, line 변수에 저장한다. 예측결과를 그래프로 표시한다.

- for: 이웃의 수가 1,3,9일 때 각각의 모델을 생성하고 학습한다.

- ax.plot(line, reg.predict(line)): line 데이터에 대한 회귀 모델의 예측 결과를 그래프로 표시한다.

- ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8) ,ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8): 학습용 데이터와 테스트용 데이터를 그래프로 표시한다. 학습용 데이터는 삼각형(^)으로, 테스트용 데이터는 역삼각형(v)으로 표시되며, 색깔은 각각 다른 색상으로 표현된다.

- ax.set_title, ax.set_xlabel, ax.set_ylabel를 사용해 각 서브플롯의 제목과 축 라벨을 설정한다.

- axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best")를 사용하여 범례를 그래프에 추가한다. Model predictions은 회귀 모델의 예측 결과, Training data/target는 학습용 데이터, Test data/target은 테스트용 데이터를 나타낸다.

--> 결과